inmotionnomad.blogg.se - Summary data two way anova in excel

SUMMARY DATA TWO WAY ANOVA IN EXCEL HOW TO

They say "B x S/A" where Prism says "residual", and say "S/A" where Prism says "subject". But note they use the term "A x B x S" where we say "Residual". Table 12.16 on page 595 explains the ANOVA table for repeated measures in one factor. Table 12.2 on page 576 explains the ANOVA table for repeated measures in both factors. When there are repeated measures for both factors, this value equals the number of subjects (3) minus 1, so df=2.ĭetails on how the SS and DF are computed can be found in Maxwell and Delaney (reference below). When the matched values are in the same row, there arr 6 subjects treated in two ways (one for each row), so df is 4. When the matched values are stacked, there are 9 subjects and three treatments, so df equals 6.

The df for subjects is the number of subjects minus number of treatments.

It is the same regardless of repeated measures.

The df for the systematic differences among columns equals number of columns -1, whiich is 2 for this example.

This is the same regardless of repeated measures.

The df for the systematic differences among rows equals number of rows -1, which is 1 for this example.

The df for interaction equals (Number of columns - 1) (Number of rows - 1), so for this example is 2*1=2.

It is the same regardless of any assumptions about repeated measures. This is the total number of values (18) minus 1. In the final columns, some of that variation can also be attributed to interaction between subjects and either rows or columns.

The SS for residual is smaller when you assume repeated measures, as some of that variation can be attributed to variation among subjects.

The SS values for the interaction and for the systematic effects of rows and columns (the top three rows) are the same in all four analyses.

This measures the total variation among the 18 values.

Now look at the SS columns for the analyses of the same data but with various assumptions about repeated measures. The last row shows the total amount of variation among all 18 values.The second to the last row shows the variation not explained by any of the other rows.The third row show the the amount of variation that is due to systematic differences between the columns.

The second row show the the amount of variation that is due to systematic differences between the two rows.Equivalently, it quantifies how much variation is due to the fact that the differences among columns is not the same for both rows. It quantifies how much variation is due to the fact that the differences between rows are not the same for all columns. The first row shows the interaction of rows and columns.

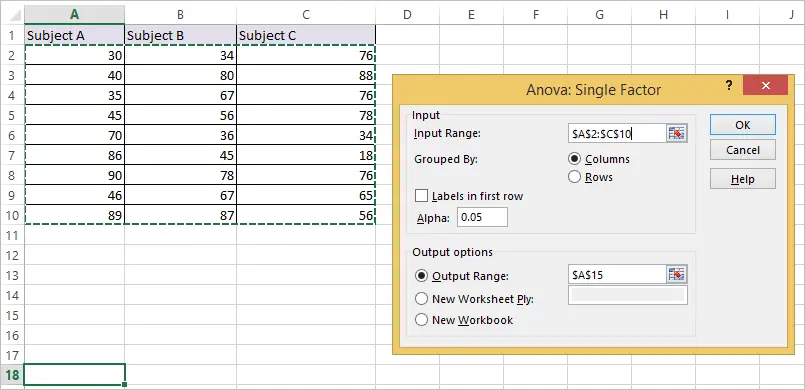
SUMMARY DATA TWO WAY ANOVA IN EXCEL HOW TO

How to report two-way ANOVA results in a table Sum-of-squaresįocus first on the sum-of-squares (SS) column with no repeated measures: I rearranged and renamed a bit so the four can be shown on one table ( Excel file). Here are the ANOVA tables for the four conditions. The colors are repeated between tables, but this means nothing.

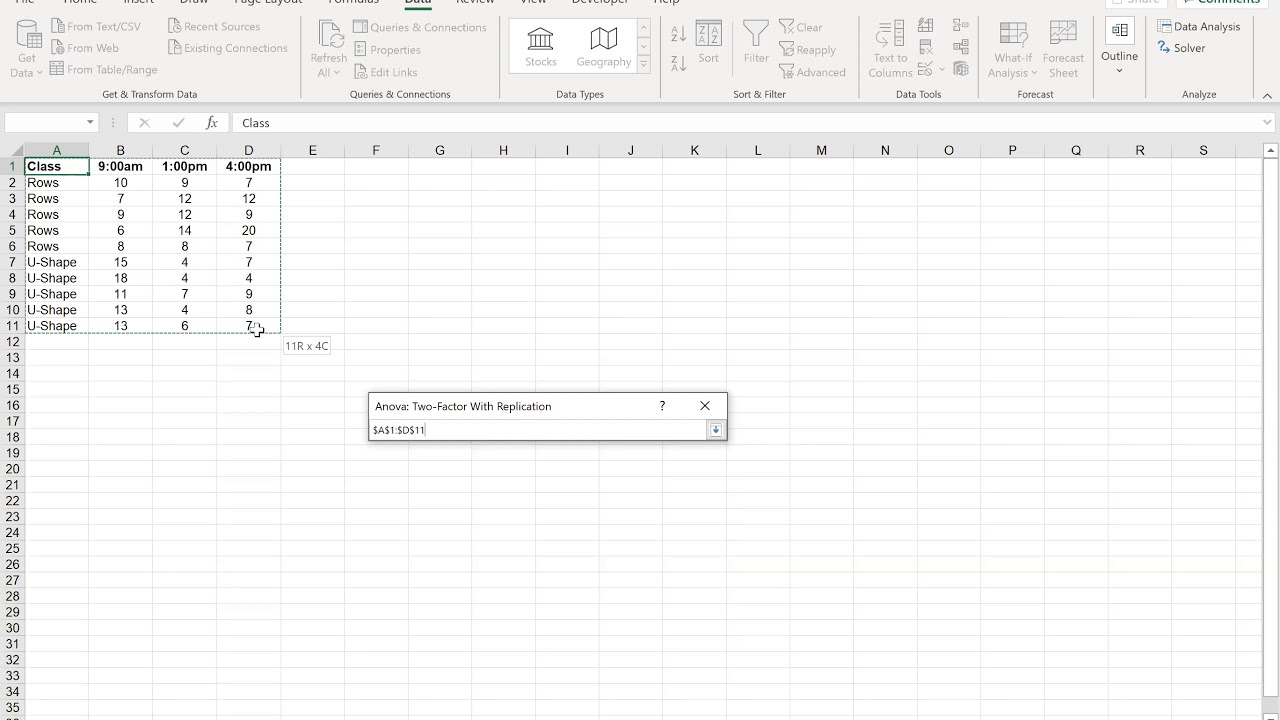
Each color within a table represents one subject. The tables below are color coded to explain these designs. I analyzed the data four ways: assuming no repeated measures, assuming repeated measures with matched values stacked, assuming repeated measures with matched values spread across a row, and with repeated measures in both directions. I entered data with two rows, three columns, and three side-by-side replicates per cell. But if you are curious in the details, this page explains how the ANOVA table is calculated. You can interpret the results of two-way ANOVA by looking at the P values, and especially at multiple comparisons.